⬆️
Кратко
Представьте себе, что у вас есть монета и шахматная доска, по которой вы можете перемещаться только вверх или только вправо. Выпадает орел – перемещаетесь вверх. Выпадает решка – перемещаетесь вправо. Очевидно, что в таком случае ваша максимально возможная скорость перемещения изменяется в зависимости от того, в каком соотношении выпадают орлы и решки. Максимальной скорость будет, если у вас выпадают только орлы или только решки. Минимальной – когда количество орлов и решек равно (в таком случает ваша скорость будет отличаться в корень из 2 раз от максимальной).
Теперь представьте себе, что вы не знаете, что ваше перемещение зависит от выпадений орла и решки. Вы считаете ваши перемещения вдоль каждой из осей независимыми друг от друга случайными величинами.
Обозначим символами na и nb вероятность событий a и b если бы они были независимыми, символами pa и pb вероятность зависимых событий a и b.
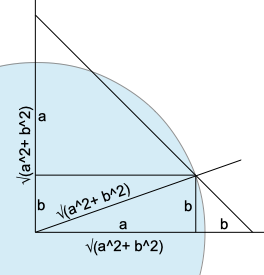
Допустим произошло a событий движения вправо и b событий движения вверх. Вы видите, что вы переместились за это время на расстояние √(a²+b²) – по теореме Пифагора.
Вы высчитываете вероятность перемещения вдоль каждой из осей: делите общее перемещение на количество событий:
na=a/√(a²+b²)
nb=b/√(a²+b²)
Таким образом у вас есть:
- “максимально возможное” перемещение вдоль каждой из осей
- фактическое перемещение вдоль каждой из осей
- подсчитанная вами вероятность 2 независимых событий перемещения
Но на самом деле они ведь зависимые! Каждый раз, когда не выпадает орел, выпадает решка и наоборот.
На данный момент мы отдельно считаем вероятность орлов и вероятность решек, как независимых случайных величин. Чтобы перейти от независимых событий к зависимым, нам необходимо добавить условие. А именно. Мы знаем вероятность независимого выпадения орла. Вероятность выпадения зависимого орла будет равна вероятности выпадения орла как независимого события при условии не происхождения не выпадения орла как независимого события. Вероятность не выпадения независимого орла = 1 – na, вероятность не происхождения события не выпадения независимого орла равна 1 – (1 – na) = na
Таким образом вероятность выпадения орла, как зависимого события, равна
pa = na*na = na² = a²/(a²+b²)
Аналогично вероятность выпадения орла, как независимого события, равна
pb=nb*nb = nb² = b²/(a²+b²)
Сумма вероятностей выпадения орла или решки равна сумме вероятностей выпадения орла при условии не выпадения решки и выпадения решки при условии не выпадения орла.
pa + pb = na² + nb²= a²/(a²+b²)+b²/(a²+b²) =(a²+b²)/(a²+b²) = 1
Такую же последовательность размышлений можно построить для 3 “независимых” событий и так же прийти к аналогичной формуле:
pa + pb + pc = na² + na² + nc² = 1
так же важно отметить, что если у нас есть например вероятность двух из 3 “независимых” событий pa и pb, то вероятность третьего “зависимого” будет равна 1-(pa+pb) = 1-(na² + na²) (смотри интерпретацию волновой функции квантовой механики)
Таким образом связь между независимыми и зависимыми вероятностями – это возведение вероятности независимого события в квадрат и извлечение корня и вероятности зависимого события. Я тут ничего нового не отрываю, в статистике это массово используется – например в “критерии хи-квадрат”.
Пример. Вернемся к конкретному примеру с орлом и решкой и перемещением по шахматной доске. Допустим выпадения орла и решки равновероятны и в результате вы перемещаетесь по диагонали.
Считая перемещения независимыми вы вычисляете вероятности перемещения вдоль каждой оси и приходите к единственно возможному в такой ситуации выводу, что вы перемещаетесь вдоль каждой из осей с вероятностью 1/√2 (примерно 0.7071). Расстояние, на которое вы при этом перемещаетесь с вероятностью 1/√2, так же равно 1/√2 (среднее перемещение за 1 бросок при перемещении по диагонали шахматной доски)
То есть за один момент времени вы в среднем продвигаетесь на 0.7071 по x и на 0.7071 по y. То есть вы считаете что вы можете одновременно передвинуться и по x и по y c вероятностью 0.7071 вдоль каждой оси.То есть могут быть такие моменты времени, когда вы передвигаетесь вдоль обеих осей, так как у вас выпали и орел и решка, а бывают такие моменты времени, когда у вас не выпало ни орла ни решки и вы остались на месте.
Но это не соответствует действительности. Правда заключается в том, что вы всегда передвигаетесь: ИЛИ вдоль оси x ИЛИ вдоль оси y в каждый момент времени в вероятностью 0.5.
Вам могут показаться странными эти, казалось бы, излишне скрупулёзные, банальные рассуждения, пока вы не попробуете вооружиться ими и погрузиться в квантовую механику.
В двух словах, в соответствии с bra-ket нотацией квантовой механики я, похоже, мог бы описать свои “независимые” орел и решку примерно так:
1/√2| орел > + 1/√2| решка >.
В соответствии с этой нотацией у меня “могут выпасть” и орел и решка одновременно за одно бросание с такими вот странными “амплитудами”. И именно такие странные события изучает квантовая механика (та самая, что “контринтуитивна”). Но чтобы перейти к вероятности эти амплитуды возводят в квадрат – так же как мы в примере выше.
Другим примером будут “независимые” перемещение в пространстве и ход часов и внезапно появляющееся замедление времени на больших скоростях (специальная теория относительности). Да, я утверждаю, что наша вселенная устроена так, что перемещение в пространстве и во времени в ней так же как выпадение орла и решки – взаимоисключающие события.
Больше информации будет предоставлено в соответствующих статьях в разделе Физика Простого мира.Отдельный интерес может представлять данная статья:
Кот Шредингера