⬆️
Допустим мы подбрасываем монетку и имеем два возможных варианта исхода: орел, решка. При этом как и ранее мы не в курсе, что события a и b зависимы (и взаимно исключают друг друга). Допустим опытным путем мы смогли установить, что вероятность события a равна pa. Вычислим вероятность события b.
Если бы мы обладали информации про зависимость событий, мы бы получили:
pb=1-pa. (1)
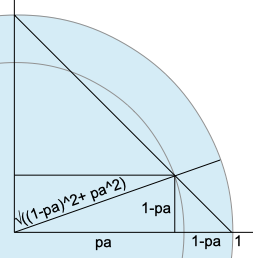
Но мы же считаем, что события независимы, потому хотим получить независимую вероятность nb. Какой должна в таком случае оказаться эта вероятность?
Зная катеты треугольника (pa, 1-pa) по аналогии с прошлой статьей получаем:
nb=pb/√(pa² + pb²) =(1-pa)/√(pa² + (1-pa)²)
Соответственно вероятность na как независимого события
na=pa/√(pa² + pb²) =pa/√(pa² + (1-pa)²)
Вероятность “зависимого события” pb’, полученного таким образом, равна
pb’ = nb² = (1-pa)² /(pa² + (1-pa)²) (2)
Имеем 2 вероятности pb и pb’. Первая – это то как все было “на самом деле”, вторая – результат ошибочного предположения, что pa и pb – независимые события.
Допyстим pa=x. Сравним графики функций (1) и (2) (спасибо Google)
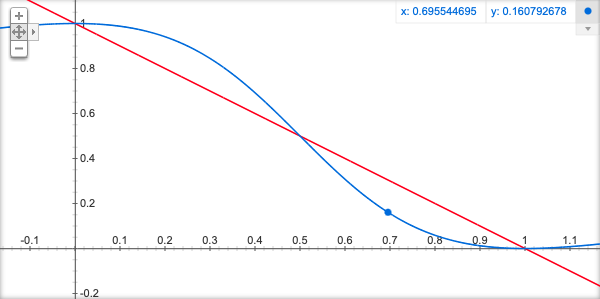
красный – (1)
Синий – (2)
Как видите, при помощи легких манипуляций, на пустом месте мы создали некую нелинейную функцию вероятности (2), которая говорит нам.. то же что (1), только очень запутанными словами. Эта функция, кстати, если ее перевести в полярные координаты, совпадает с предсказаниями квантовой механики из теоремы Белла. Допустим t меняется от 0 до pi/2. Выразим x через этот угол.
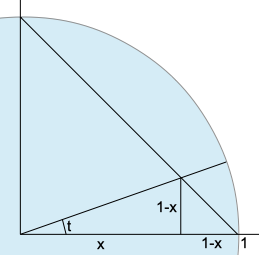
tg(t)=x/(1-x)
tg(t) -tg(t)x=x
x=tg(t)/(1 +tg(t))
подставляем в формулу и получаем график:
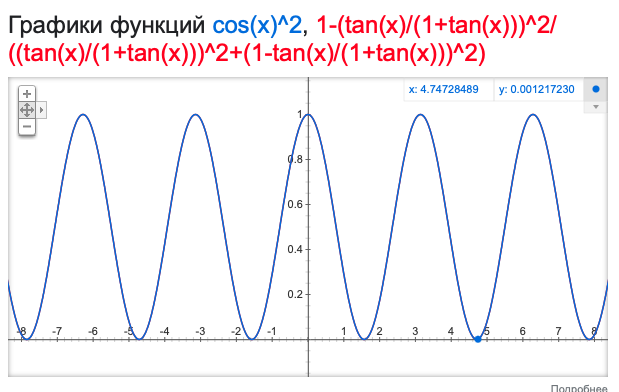
Не удивительно, что он совпадает с cos(x)^2 – который, на сколько я понимаю, связан с предсказаниями квантовой механики.
Квантовая механика считается загадочной, контринтуитивной и нелокальной. Но возможно в ней просто таким же образом некоторые зависимый события ошибочно приняты за независимые.
И больше ничего..